การคำนวน Numpy dot product หรือ การคูณเมทริก (Matrix Multiplication)

การคูณเมทริก

• แถว ของตัวตั้ง = หลักของตัวคูณ
• ผลที่ได้ทำให้ Dimension เปลี่ยนไป

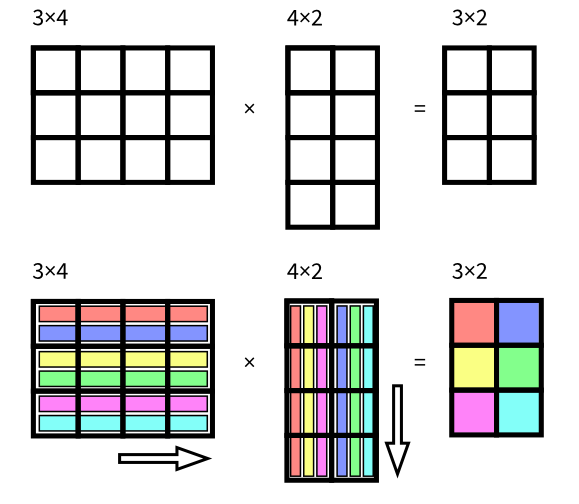
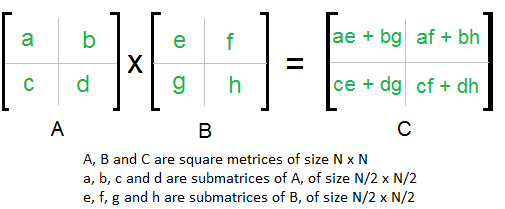
ตัวอย่างการหาผลคูณ Matrix

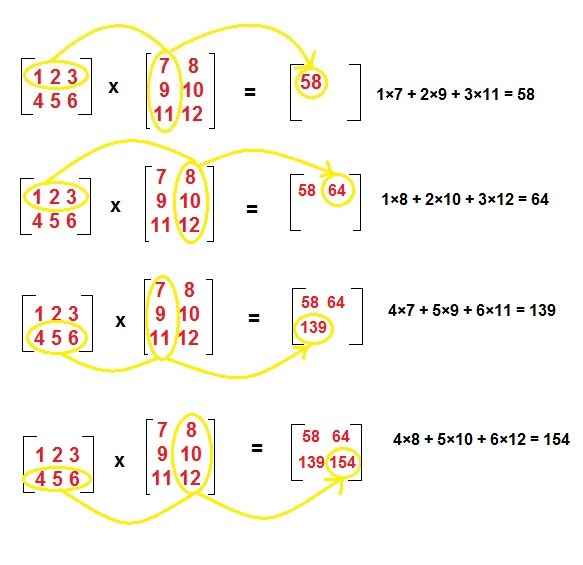
การคูณเวกเตอร์

การคุณเวกเตอร์ทำได้ 2 ประเภท

• dot (.) ผลที่ได้เป็น scalar product

• cross (x) ผลที่ได้เป็น Vector Poduct

Dot product

นิยาม1:

| 1,3,5 | และ |4,-2,-1| แทน ด้วย 1x + 3y +5z และ 4x -2y -1z

นิยาม2:

ตัวอย่างเป็นการหาค่าของ a.b (a dot b) ของ vector a และ vector b

# Array a = [1,3,-5]
a = np.array([1,3,-5])

# Array b = [4,-2,-1]
b = np.array([4,-2,-1])


# ผลคูณของ a * b = a0b0 + a1+b1 + ... + a(n)*b(n)
dot = a.dot(b)

หรือคำนวนโดยวิธีการด้านล่าง ก็ให้ผลเท่ากัน

# ตัวอย่าง
a = [1,3,-5]
b = [4,-2,-1]

np.dot(a,b)

# ตัวอย่าง
a=np.array([3,-5,+6])
b=np.array([0,2,0])

a.dot(b)

Cross product

เป็นการคูณ เวกเตอร์ชนิดหนึ่่งโดยผลที่ได้จะเป็นเวกเตอร์เช่นเดียวกัน

# ตัวอย่าง vector หนึ่งหน่วย
x = np.array([0,0,1])
y = np.array([0,1,0])

np.cross(x,y)
np.cross(y,x)

สูตรการ cross

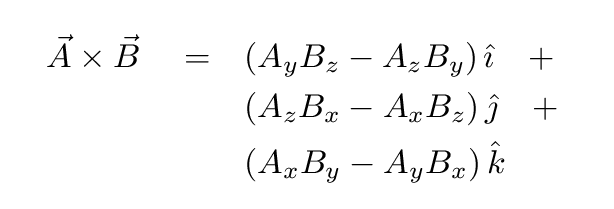
# ตัวอย่าง cross 3d
x = [1, 2, 3]
y = [4, 5, 6]
np.cross(x, y)

การบวกลบเวกเตอร์ (Vector addition and subtraction)

การนำเวกเตอร์ มาบวก หรือ ลบ นั้นสามารถแสดงได้ด้วย รูปภาพโดยนำเอา หาง tail ของ y มาต่อกับหัว head ของ x

 x = np.array([3,2])
 y = np.array([5,1])
 z = x + y
 z

z = x - y
z

การหา inverse matrix

นิยม ของ Inverse ของ matric คือ matrix ที่เมือนำมาคูณกับ matric ตั้งต้นแล้ว จะได้เป็น เมทริก เอกลักษณ์ (identity matrix) โดยการหา Inverse จะใช้ ฟังก์ชั่น numpy.linalg.inv()

x = np.array([[1,2],[3,4]]) 
y = np.linalg.inv(x) 
x 
y 
np.dot(x,y)

การหาค่า determinant ของ matric

ค่า deteminant สามารถหาได้จาก numpy.linalg.det(a)

 a = np.array([[4, 2, 0], [9, 3, 7], [1, 2, 1]], float)
 a
 np.linalg.det(a)